# Básico do básico: ponteiros

2008-12-06 tag_coding ^ ctrl_c

Nessas últimas semanas tenho gastado meu tempo junto da mais nova pupila da SCUA, aspirante a programadora em C e Install Shield Script. Minha tarefa? Explicar tudo, desde o mais simples, como **variáveis**, até as coisas não tão triviais, como **símbolos de depuração**.

Posso afirmar que tem sido muito compensador ativar algumas partes do meu cérebro que acreditava nem mais existirem. Rever velhos conceitos, apesar de manjados, nos dá a oportunidade de lembrar que as coisas mais complexas que construímos no dia-a-dia se baseiam em um punhado de preceitos básicos que é essencial ter na cabeça. E nunca esquecê-los.

Meu amigo costuma chamar esses preceitos básicos de **fundamentais**. Isso por um bom motivo lógico e semântico: tudo que aprendemos de básico sobre qualquer área de conhecimento serve-nos de **base** para suportar as outras coisas que virão a ser entendidas na mesma área de conhecimento. Ou seja: é **a parte mais importante a ser aprendida**. Sem ela, a base, não nos é possível construir nada **sólido** e **duradouro**. Sem ela, toda a estrutura construída _a posteriori_ se rompe e vai abaixo.

Foi partindo desse princípio que me preocupei com esmero para explicar as peças mais fundamentais do conhecimento em jogo, formadoras da cabeça de um programador para sempre, seja em C como em qualquer outra linguagem. E como nada é bem explicado sem formar imagens na cabeça, aproveitei para desenhar alguns esboços no papel. O resultado desses esboços é esse artigo.

Ponteiro: o eterno vilão da história

Não tenho a presunção de conseguir explicar 100% para alguém iniciante o que são ponteiros em C, como usá-los e como se proteger deles. Definitivamente ponteiro não é um conceito simples, apesar de básico, e posso dizer sem vergonha que demorei cerca de seis meses no meu aprendizado em C pra entender completamente tudo relacionado com ponteiros. Demorou, quebrei a cabeça, mas depois nunca mais esqueci.

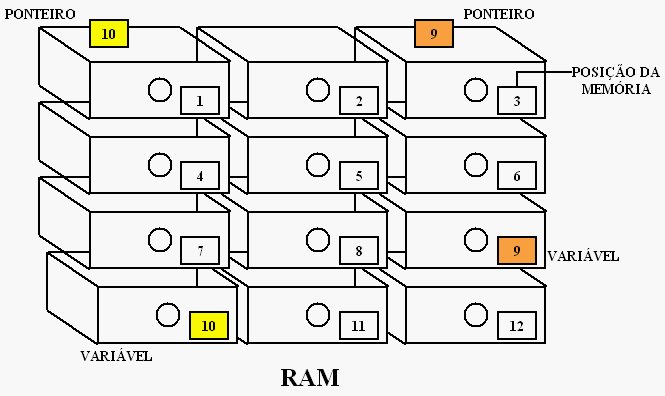
De acordo com o meu amigo Rafael, a melhor definição que usei até hoje para explicar esse conceito envolvia um armário repleto de gavetas, todas numeradas em ordem de posição (1, 2, 3...). Cada gaveta podia guardar qualquer coisa, inclusive o número de outra gaveta em um pedaço de papel. Com isso, eu poderia guardar em uma gaveta aleatória o que eu precisava guardar e escrever o "endereço" dessa gaveta em um pedaço de papel e guardá-lo na gaveta número 1, por exemplo. Com isso poderia até esquecer a posição onde está o que eu guardei, pois bastava abrir a gaveta número 1 e ler a posição em que estava essa gaveta.

Deve ter ficado óbvio, mas se não ficou: o armário é a memória RAM, as gavetas são váriáveis e as gavetas onde guardamos pedaços de papel são ponteiros, que não deixam de ser variáveis, e apontam para outras gavetas que são... adivinha? Outras variáveis!

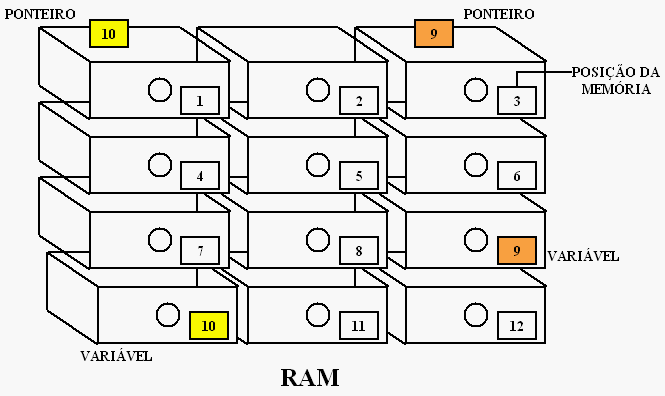
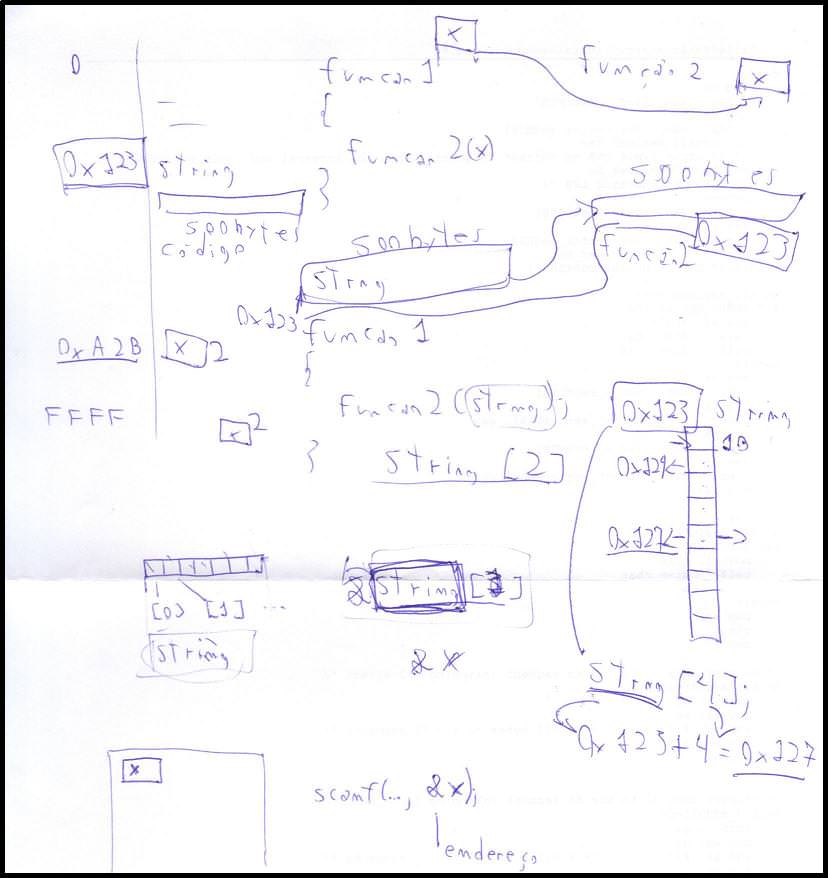
Outros conceitos que costumo utilizar é relacionar a memória RAM com a memória do programa e contar a memória como se contam carneirinhos. Dessa forma fica fácil pelo menos entender dois conceitos fundamentais na arte dos ponteiros: memória e endereço.

Practice makes perfect

O segundo passo, acredito eu, é entender como a memória é dimensionada através do programa, e como o tipo molda a representação dos bits e bytes através das ligações de silício, mas isso fica pra mais tarde. Temos que programar, e é isso que vai de fato fazer a diferença no aprendizado de uma linguagem como C. Nada como uma boa mistura de teoria e prática para gerar um concreto armado que irá suportar um Empire State de conhecimento.

Por isso, segue uma lista de tarefas interessantes para exercitar o conceito de ponteiros:

* Criar funções que modificam números passados como parâmetro.

* Criar funções que modificam texto passado como parâmetro.

* Alocar e desalocar memória dinamicamente.

Tarefas mais específicas da minha área e que uso o tempo todo:

* Escrever e ler texto em arquivos.

* Escrever e ler no registro do Windows.

* Obter o endereço de uma função do Windows dinamicamente. E chamá-la.

Nota: Não use as classes superiores de C++ nem referências. Estou falando de estudar ponteiros nua e cruamente. Não seja preguiçoso. Algumas coisas devem ser feitas da maneira mais "primitiva" até se entender com o que se está lidando. Lembre-se que os melhores programadores possuem os alicerces mais fortes.

Bônus Points: Fantoches!

Este vídeoab_channel=Napalm">vídeo é o mais didático do universo sobre como funcionam ponteiros em C. Veja e mostre pros seus filhos.

# Básico do básico: tipos

2008-12-12 tag_coding ^ ctrl_c

Um tipo nada mais é que do que uma forma (ô) de bolo, que **molda a memória** como acharmos melhor moldá-la. Bom, para isso fazer sentido é necessário explicar memória, que é um conceito **mais básico ainda**.

A memória é **qualquer lugar** onde eu possa **guardar alguma coisa**. No artigo anterior era um punhado de gavetas. Mas poderiam muito bem ser caixas de presente. Ou um caderno. Ou até uma placa de memória RAM. O que sua criatividade quiser.

O importante no conceito de memória, computacionalmente falando, é saber que ela pode guardar qualquer tipo de informação, mas ela **não sabe o que você está guardando**. E eis que surge o segredo do **tipo**: ele conta para você, e seu programa, o que de fato está guardado na memória.

Vamos exemplificar.

Este artigo é um punhado de números na memória

Computadores trabalham muito bem com números. A própria memória só guarda valores numéricos. Porém, se é dessa forma, como conseguimos abrir o Bloco de Notas e digitar algum texto?

Para entender essa "mágica" é necessário vir à tona o conceito de **representação**, um tema que ainda pode dar muito pano pra manga quando estudarmos base numérica. Por enquanto, basta saber que uma representação é um **faz-de-conta** em que todos concordam com o que for dito. Por exemplo: Faz de conta que a letra 'A' é o número 65. Dessa forma, sempre que for visto o número 65, de agora em diante, será vista a letra 'A' no lugar.

Existem alguns faz-de-conta que são muito difundidos entre e humanidade informática. Um deles é chamado **tabela ASCII** (se pronuncia "ásqui"). É uma forma de todos conseguirem entender os textos de todo mundo. Abaixo podemos ver a representação de todas as letras maiúsculas na codificação ASCII:

Número Letra

====== =====

65 A

66 B

67 C

68 D

69 E

70 F

71 G

72 H

73 I

74 J

75 K

76 L

77 M

78 N

79 O

80 P

81 Q

82 R

83 S

84 T

85 U

86 V

87 W

88 X

89 Y

90 Z

Agora, imagine que você digitou o seguinte texto no bloco de notas:

CASA

Como esse texto é guardado na memória de um computador, se ele só entende números?

Através da nossa já conhecida tabela ASCII! Na verdade, números são armazenados na memória, mas por representarem as letras 'C', 'A', 'S' e 'A', são traduzidos de volta para o formato texto pelo Bloco de Notas, que conhece o que guardou na memória.

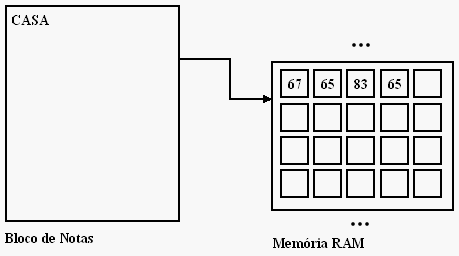
A memória pode guardar qualquer coisa com números

A técnica de representação pode guardar qualquer coisa na memória como números que serão traduzidos por algum programa que consiga abrir aqueles dados. Dessa forma podemos não só armazenar texto, como imagens, vídeos, páginas web e até mesmo os próprios programas que os abrem!

Na programação do dia-a-dia, as coisas funcionam da mesma forma. As tão faladas variáveis reservam um espaço de memória para guardar alguma coisa, mas só sabemos o que essa alguma coisa é através do tipo da variável:

// a variável idade (espaço de memória)

// pode guardar um número (tipo)</font>

int idade;

// a variável nome (espaço de memória) pode

// guardar o nome de alguém de até 99 letras (tipo)

char nome100;

// a variável cad (espaço de memória) pode

// guardar o cadastro de uma pessoa (tipo)

Cadastro cad;

Esses elementos, na memória, são um bando de número que, sem os tipos, não possuem significado algum, como podemos ver na depuração do programa abaixo:

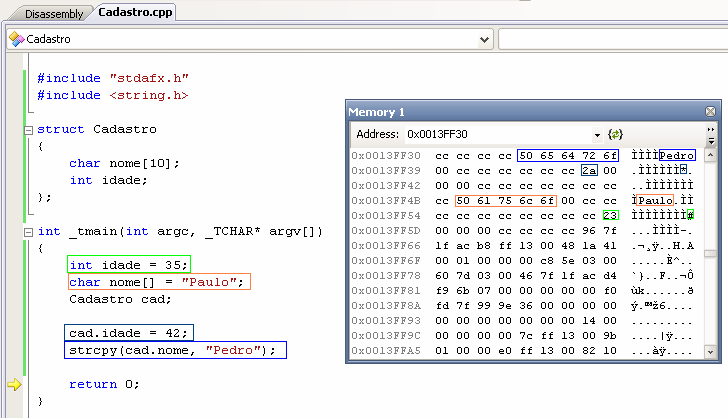
Note que os números não estão aqui representados em decimal, onde se esperaria 35 e 42, pois a representação formal da memória geralmente está no formato hexadecimal, transformando esses números em 0x23 e 0x2a, respectivamente. Para entender essa diferença cabe estudar um pouco sobre base numérica, outro tema básico do programador sólido.

Practice makes perfect

Nada é bem aprendido se não for apreendido. Algumas tarefas programáticas que podem fixar o conceito de tipo estão listadas abaixo:

* Usar **printf **especificando tipos diversos (%d, %s, %f, %p, ...) para a mesma variável, inclusive correndo o risco de gerar algumas exceções.

* Usar **scanf** especificando diversas variáveis para o mesmo tipo (%d, %s, %f, %p, ...), vendo o resultado da leitura da entrada do usuário na memória.

* Tentar copiar o conteúdo de uma variável para outra variável de **tipo diferente**. Sempre analise a memória para ver o resultado.

Outros faz-de-conta bem famosos

* Ordenação de extremidades: O problema Little Endian e Big Endian.

* UNICODE: Por um conjunto de letras universal.

* Base numérica: O que são binário e hexadecimal e como eles afetam nossa vida.

# Básico do básico: binário

2008-12-18 tag_coding ^ ctrl_c

Apesar do tema binário, o assunto de hoje no fundo remete-nos a todo e qualquer tipo de **representação**. É o faz-de-conta um pouco mais intenso, vindo das profundezas da matemática e dominado com maestria pela nossa mente e sua capacidade lógica de abstrair.

Como todos sabemos, nós, seres humanos, somos dotados de dez dedos: cinco em cada mão. Isso influenciou fortemente nosso sistema de contagem de coisas, e, como consequência, nossa forma de representar números.

No entanto, números serão sempre números, independente de seres humanos e de dedos. Outros seres inteligentes de outras galáxias poderiam representar os mesmo números, sendo um conceito lógico independente de raça, usando qualquer outra forma e quantidade de símbolos. Por falar em símbolos, nós temos **dez**, a saber:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Outros seres poderiam usar, sei lá, dois:

0, 1

É lógico que esse '0' e esse '1' podem ser representados por outros sinais, como pedra e pau, cara e coroa, tico e teco, e por aí vai a valsa.

O importante é que seriam na quantidade de **dois**.

Último detalhe

O nosso sistema de representação ainda possui algumas características singulares, como o **valor posicional**. Os mesmos dez símbolos, quando colocados em **posições diversas**, assumem **valores diversos**.

Dessa forma, quando esgotamos todos os símbolos e chegamos a nove, para irmos ao dez começamos a repetir os símbolos, mas em outra posição:

 7,

 8,

 9,

10!

A nova posição do símbolo '1' possui o próximo valor após o nove. O zero, como sabemos, apenas **marca posições** e não possui valor algum. Se valesse algo, seria somado, como no número 111, que é uma **soma de três valores distintos posicionados de acordo**:

100 +

10 +

1

===

111

Pronto! Eis toda a base de nosso sistema numérico. O resto é historinha pra boi dormir. Com isso é possível até mudarmos de base, ou seja, o número de símbolos usados, conforme nos convier.

Mudando de base

Para nos comunicarmos com a raça alienígena que usa dois símbolos poderíamos contar seguindo o mesmo princípio:

0,

1,

10,

11,

100,

101,

110,

111,

...

O valor do número, como sabemos, depende de sua posição. Mas, calma lá! O 111 logo acima não é idêntico ao 111 que vimos anteriormente, pois **mudamos a base**! Agora só temos dois símbolos para representar números, quando antes tínhamos dez.

O "segredo" do valor posicional também está na base, pois o zero, apesar de não possuir valor, marca a quantidade de símbolos que foram utilizados para se esgotar uma posição qualquer. Dessa forma, enquanto o nosso conhecido 10 (dez) vale todos os símbolos não-nulos (nove) mais um (nove + um = dez), o outro 10 (um-zero) da raça alienígena de dois dedos também vale todos os símbolos deles nã-nulos (um) mais um (um + um = dois).

Contando em binário?

Como não faz parte do tema, não vou explicar como o sistema binário foi importante para a definição de uma arquitetura simples o suficiente para ser expandida a níveis nunca antes imaginados de processamento e comprimida em espaços que muitos diriam não caber qualquer coisa de útil que fosse. No entanto, apesar de brilhante, o binário no dia-a-dia do programador gera alguns problemas. Principalmente se o programador escreve seus cálculos de **ponteiros em binário**.

Para entender isso, basta lembrar que, atualmente, a quantidade de memória RAM que é contada e, portanto, valor dos ponteiros que apontam para ela, é muito grande **até **para nosso sistema decimal, que possui, relembrando, dez símbolos. O que dirá, então, um sistema que possui meros dois símbolos para representar, digamos, **três gigabytes**:

11000000000000000000000000000000

São tantos zeros que aqueles bugs de _leak _de memória, famosos por levar tempo para ser corrigidos, seriam mais famosos ainda, pois o tempo gasto para se entender alguma coisa no meio de ponteiros dessa magnitude seria astronômico!

E, claro, ainda poderia ficar pior, se fosse depurado um desses novíssimos sistemas de 64 bits:

10011101101101101101101101101101101101101101

Contando de dezesseis em dezesseis

Eu sei que não vou conseguir explicar tudo sobre bases numéricas em apenas um miniartigo. Porém, vamos dar uma rápida olhada no famoso hexadecimal, que foi o que nos salvou de lidar com os numerozinhos acima.

Nesse sistema, a representação dos número ocupa **menos espaço ainda** que o sistema decimal, pois usa **dezesseis **símbolos distintos, usando as letras de A a F após os já conhecidos símbolos decimais:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

A grande vantagem de contar as coisas em dezesseis é que sua representação **será sempre um múltiplo de dois**, o que facilita a conversão para o sistema binário: em um único número hexadecimal cabem quatro números binários, ou **quatro bits**.

Bin. Hexa Dec.

0000 0 0

0001 1 1

0010 2 2

0011 3 3

0100 4 4

0101 5 5

0110 6 6

0111 7 7

1000 8 8

1001 9 9

1010 A 10

1011 B 11

1100 C 12

1101 D 13

1110 E 14

1111 F 15

Tabelinha básica, fácil de achar em qualquer lugar da internet, mas colocada aqui apenas para relembrar a relação entre as três bases.

Bom, acho que é isso. Já ultrapassei o limite do teórico, porque na verdade o que importa aqui, para captar de fato o binário dos fatos, é **praticar**:

Coisas para pensar a dois

* Conte em binário quando não estiver fazendo nada. É simples e ajuda a fixar. Dessa forma: um, um-zero, um-um, um-zero-zero, um-um-zero, um-um-um, ...

* Decore a relação entre os números hexadecimal e binário. Você pode até esquecer isso depois, mas o esforço para decorar será útil para fixar. E nunca se sabe quando você terá que reaver a MBR de um cliente seu.

* Estude a lógica por trás da tabela ASCII e seus valores binários. Irá descobrir que existem relações muito óbvias entre letras, números (maíusculos e minúsculos) e sinais. Tente decorar.

# HouaissParaBabylon versão 1.1

2008-12-30 ^ ctrl_c

Saindo mais um do forno.

Essa nova versão do conversor do dicionário Houaiss para Babylon corrige o problema de não encontrar o Houaiss 1.0. O problema ocorria porque o conversor se baseava na localização do desinstalador para encontrar o dicionário. Na primeira versão do dicionário o desinstalador fica na pasta c:\Windows, onde obviamente não estava o dicionário.

Nessa nova versão, além de procurar o caminho do dicionário no registro (desinstalador) e antes de pedir para o usuário o caminho correto é tentado o caminho padrão de instalação, %programfiles%\Houaiss. Se mesmo assim o dicionário não existir continuamos perguntando para o usuário, que tem a opção de dizer onde está instalado o dicionário no disco rígido ou apontar diretamente para o CD de instalação.